赋可列半范线性空间

　　设E是局部凸空间，如果E的拓扑可由可列个连续半范数{pn(∙)}确定，则称E是赋可列半范线性空间。

　　简介

　　赋可列半范线性空间是一类局部凸空间。

　　设E是局部凸空间，如果E的拓扑可由可列个连续半范数{pn(∙)}确定，则称E是赋可列半范线性空间。不失一般性，还可以要求p1(x)≤p2(x)≤...≤pn(x)≤...(x∈E)。

　　当pn都是范数时，称E为赋可列范线性空间。1

　　判定

　　局部凸空间为赋可列半范空间的充分必要条件是存在可列的零元邻域基。

　　赋可列半范空间是准范空间，巴拿赫空间上的算子理论大部分可以推广到这类空间上。

　　半范数

　　半范数是范数的一种推广，其比范数的要求弱（半范数比范数少一个条件：使半范数值为0的元素不一定是0元素），范数一定是半范数。局部凸线性空间的拓扑可以由一族满足分离公理的半范数来确定。

　　设p是定义于线性空间X上的非负实值函数，满足：

　　（1）

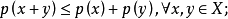
　　（2）

　　则称p是X上的一个半范数，X称为赋半范线性空间。

　　本词条内容贡献者为:

　　李嘉骞 - 博士 - 同济大学