可赋范拓扑线性空间

　　可赋范拓扑线性空间（normable topological linear space）是指可用范数来刻画拓扑的拓扑线性空间。

　　简介

　　可赋范拓扑线性空间是指可用范数来刻画拓扑的拓扑线性空间。

　　设E是拓扑线性空间，如果E上还存在一个范数||·||，使||·||导出的拓扑与E中原来的拓扑相同，则称E是可赋范的。1

　　判定

　　拓扑线性空间可赋范的充分必要条件是满足下面三条：

　　1.E满足T0公理；

　　2.E是局部凸的；

　　3.E是局部有界的。

　　上述充分必要条件是柯尔莫哥洛夫于1934年给出的，也是最早得到的有关拓扑线性空间理论的一个结果。

　　拓扑线性空间

　　设X为实数域或复数域K上的线性空间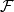，是X上的拓扑，如果

　　（1）加法是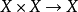的连续映射；

　　（2）数乘是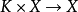的连续映射；

　　则称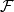是X上的向量拓扑或线性拓扑，称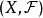为拓扑线性空间或拓扑向量空间。

　　注：1）零元的均衡的邻域全体组成零元的邻域基。

　　2）满足T1分离公理的拓扑线性空间是完全正则的。

　　本词条内容贡献者为:

　　李嘉骞 - 博士 - 同济大学